Permutasjoner og kombinasjoner matematikk

Permutasjoner og kombinasjoner, de forskjellige måtene objekter fra et sett kan velges, vanligvis uten erstatning, for å danne undergrupper. Dette valget av undergrupper kalles en permutasjon når rekkefølgen på valg er en faktor, en kombinasjon når rekkefølge ikke er en faktor. Ved å vurdere forholdet mellom antall ønskede undergrupper og antall alle mulige undergrupper for mange sjansespill på 1600-tallet ga de franske matematikerne Blaise Pascal og Pierre de Fermat drivkraft til utviklingen av kombinatorikk og sannsynlighetsteori.

kombinatorikk: Binomiale koeffisienter

n objekter kalles en permutasjon av n ting tatt r om gangen. Antall permutasjoner er

Konseptene og forskjellene mellom permutasjoner og kombinasjoner kan illustreres ved å undersøke alle de forskjellige måtene et par objekter kan velges fra fem forskjellige objekter - for eksempel bokstavene A, B, C, D og E. Hvis begge deler bokstavene som er valgt og rekkefølgen på valg blir vurdert, så er følgende 20 utfall mulig:

Hver av disse 20 forskjellige mulige valgene kalles en permutasjon. Spesielt kalles de permutasjoner av fem objekter tatt to om gangen, og antallet slike mulige permutasjoner er betegnet med symbolet ₅ P ₂, les “5 permute 2.” Generelt, hvis det er n objekter tilgjengelige å velge fra, og permutasjoner (P) skal dannes ved bruk av k av objektene om gangen, blir antallet forskjellige mulige permutasjoner betegnet med symbolet _n P _k. En formel for evaluering er _n P _k = n! / (N - k)! Uttrykket n! —Les “n factorial” - indikerer at alle påfølgende positive heltall fra 1 til og med n skal multipliseres sammen, og 0! er definert til lik 1. For eksempel, ved bruk av denne formelen, er antall permutasjoner av fem objekter tatt to om gangen

(For k = n, _n P _k = n! Altså, for 5 objekter er det 5! = 120 ordninger.)

For kombinasjoner velges k-objekter fra et sett med n-objekter for å produsere undergrupper uten å bestille. I motsetning til forrige permutasjonseksempel med den tilsvarende kombinasjonen, er AB- og BA-undergruppene ikke lenger forskjellige valg; ved å eliminere slike tilfeller gjenstår det bare 10 forskjellige mulige undergrupper - AB, AC, AD, AE, BC, BD, BE, CD, CE og DE.

Antallet slike undergrupper er angitt med _n C _k, les “n velg k.” For kombinasjoner, siden k objekter har k! ordninger, det er k! Utskillbare permutasjoner for hvert valg av k-objekter; følgelig dele permutasjonsformelen med k! gir følgende kombinasjonsformel:

Dette er det samme som (n, k) binomial koeffisient (se binomial teorem). For eksempel er antall kombinasjoner av fem objekter tatt to om gangen

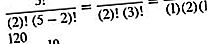
Formlene for _n P _k og _n C _k kalles telleformler siden de kan brukes til å telle antall mulige permutasjoner eller kombinasjoner i en gitt situasjon uten å måtte liste dem alle.